Sifat Tertutup
Sifat tertutup maksudnya bahwa pada perkalian pada bilangan pecahan, akan selalu menghasilkan bilangan pecahan juga. Hal ini dapat dituliskan bahwa “Untuk setiap bilangan pecahan p dan q, selalu berlaku p × q = r dengan r juga bilangan pecahan”.
Contoh Soal 1
a. (3/5) × (8/11) = 24/55
di mana kita ketahui bahwa 3/5 dan 8/11 merupakan bilangan pecahan dan 24/55 juga merupakan bilangan pecahan.
b. 3/5 × (–8/11) = –24/55
di mana kita ketahui bahwa 3/5 dan –8/11 merupakan bilangan pecahan dan –24/55 juga merupakan bilangan pecahan.
c. (–3/5) × 8/11 = –24/55
di mana kita ketahui bahwa –3/5 dan 8/11 merupakan bilangan pecahan dan –24/55 juga merupakan bilangan pecahan.
d. (–3/5) × (–8/11) = 24/55
di mana kita ketahui bahwa –3/5 dan –8/11 merupakan bilangan pecahan dan 24/55 juga merupakan bilangan pecahan.
Sifat Komutatif (Pertukaran)
Operasi perkalian dua bilangan pecahan selalu diperoleh hasil yang sama walaupun kedua bilangan tersebut dipertukarkan tempatnya. Hal ini dapat dituliskan bahwa “Untuk setiap bilangan pecahan p dan q, selalu berlaku p × q = q × p”.
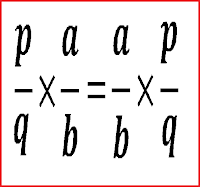
Contoh Soal 2
a. 2/3 × (–5/7) = (–5/7) × 2/3 = –10/21
b. (–3/7) × (–4/5) = (–4/5) × (–3/7) = 12/35
Sifat Asosiatif (Pengelompokan)
Sifat ini menyatakan bahwa “Untuk setiap bilangan pecahan p, q, dan r selalu berlaku (p × q) × r = p × (q ×r)”.
Contoh Soal 3
a. 3/5 × (–2/7 × 4/5) = (3/5 × (–2/7)) × 4/5 = –24/175
b. (–2/7 × 6/5) × 4/11 = –2/7 × (6/5 × 4/11) = –48/385
Sifat Distributif Perkalian Terhadap Penjumlahan
Sifat ini menyatakan bahwa “Untuk setiap bilangan pecahan p, q, dan r selalu berlaku p × (q + r) = (p × q) + (p × r)”.
Contoh Soal 4
a. 2/3 × (4/3 + (–3/3)) = 2/3 × 1/3 = 2/9
=>(2/3 × 4/3) + (2/3 × (–3/3)) = 8/9 – 6/9 = 2/9
Jadi, 2/3 × (4/3 + (–3/3)) = (2/3 × 4/3) + (2/3 × (–33/)) = 2/9
b. (–3/7) × (–8/7 + 5/7) = (–3/7) × (–3/7) = 9/49
=>((–3/7) × (–8/7)) + (–3/7 × 5/7) = 24/49 – 14/49 = 9/49
Jadi, (–3/7) × (–8/7 + 5/7) = ((–3/7) × (–8/7)) + (–3/7× 5/7) = 9/49
Sifat distributif perkalian terhadap pengurangan
Sifat ini menyatakan bahwa “Untuk setiap bilangan pecahan p, q, dan r selalu berlaku p × (q – r) = (p × q) – (p × r)”.
Contoh Soal 5
a. 5/7 × (8/7 – (–3/7)) = 5/7 × 11/7 = 55/49
=>(5/7 × 8/7) – (5/7 × (–3/7)) = 40/49 – (–15/49) = 55/49
Jadi, 5/7 × (8/7 – (–3/7)) = (5/7 × 8/7) – (5/7 × (–3/7)) = 55/49
b. 6/5 × (–7/5 – 4/5) = 6/5 × (–11/5) = –66/25
=> (6/5 × (–7/5)) – (6/5 × 4/5) = –42/25 – 24/25 = –66/25
Jadi, 6/5 × (–7/5 – 4/5) = (6/5 × (–7/5)) – (6/5 × 4/5) = –66/25
Mempunyai Elemen Identitas
Bilangan 1 (satu) merupakan elemen identitas pada perkalian. Artinya, untuk sebarang bilangan pecahan apabila dikalikan 1 (satu), hasilnya adalah bilangan itu sendiri. Hal ini dapat dituliskan bahwa “Untuk setiap bilangan pecahan p, selalu berlaku p × 1 = 1 × p = p”.
Invers Perkalian
Invers perkalian ini akan diterapkan pada operasi pembagian pada pecahan. Sekarang perhatikan perkalian bilangan pecahan berikut ini.
=> 7/5 × 5/7 = 1
=> - 2/7 × - 7/2 = 1
Pada perkalian-perkalian bilangan di atas, 7/5 adalah invers perkalian (kebalikan) dari 5/7. Sebaliknya, 5/7 adalah invers perkalian (kebalikan) dari 7/5. Secara umum dapat dituliskan bahwa invers perkalian dari pecahan p/q adalah q/p atau invers perkalian dari q/p adalah p/q, dan hasil kali suatu bilangan dengan invers (kebalikan) bilangan itu sama dengan 1.
Contoh Soal 6
Tentukan invers perkalian bilangan-bilangan berikut.
a. 3
b. –4
c. 4/9
d. 2¾
Penyelesaian:
a. 1/3
b. –¼
c. 9/4 = 2¼
d. Ubah pecahan campuran menjadi pecahan biasa yakni 2¾ = 11/4, maka invers perkalian dari 11/4 adalah 4/11.
SUMBER : http://ariyamatematika.blogspot.co.id/p/sifat-sifat-perkalian-pada-pecahan.html










0 komentar:
Posting Komentar